Hur man lägger till ett positivt tal till ett negativt tal. Subtrahera ett negativt tal, regel, exempel

I det här materialet kommer vi att beröra ett så viktigt ämne som att lägga till negativa siffror. I det första stycket kommer vi att berätta den grundläggande regeln för denna åtgärd, och i det andra kommer vi att titta på specifika exempel på att lösa sådana problem.

Yandex.RTB R-A-339285-1

Grundregel för att lägga till naturliga tal

Innan vi härleder regeln, låt oss komma ihåg vad vi generellt vet om positiva och negativa tal. Tidigare var vi överens om att negativa tal ska uppfattas som skuld, förlust. Modulen för ett negativt tal uttrycker den exakta storleken på denna förlust. Då kan tillägget av negativa tal representeras som ett tillägg av två förluster.

Med hjälp av detta resonemang formulerar vi grundregeln för att lägga till negativa tal.

Definition 1

För att slutföra lägga till negativa tal, måste du lägga ihop värdena för deras moduler och sätta ett minus framför resultatet. I bokstavlig form ser formeln ut som (− a) + (− b) = − (a + b) .

Baserat på denna regel kan vi dra slutsatsen att att lägga till negativa tal liknar att lägga till positiva, bara i slutändan måste vi få ett negativt tal, eftersom vi måste sätta ett minustecken framför summan av modulerna.

Vilka bevis kan ges för denna regel? För att göra detta måste vi komma ihåg de grundläggande egenskaperna för operationer med reella tal (eller med heltal eller med rationella tal - de är samma för alla dessa typer av tal). För att bevisa det behöver vi bara visa att skillnaden mellan vänster och höger sida av likheten (− a) + (− b) = − (a + b) kommer att vara lika med 0.

Att subtrahera ett tal från ett annat är detsamma som att lägga till samma motsatta tal till det. Därför, (− a) + (− b) − (− (a + b)) = (− a) + (− b) + (a + b) . Kom ihåg att numeriska uttryck med addition har två huvudegenskaper - associativa och kommutativa. Då kan vi dra slutsatsen att (− a) + (− b) + (a + b) = (− a + a) + (− b + b) . Eftersom vi, genom att lägga till motsatta tal, alltid får 0, då (− a + a) + (− b + b) = 0 + 0, och 0 + 0 = 0. Vår likhet kan anses bevisad, vilket betyder att regeln för lägga till negativa tal Vi bevisade det också.

I det andra stycket kommer vi att ta specifika problem där vi behöver lägga till negativa tal, och vi kommer att försöka tillämpa den inlärda regeln på dem.

Exempel 1

Hitta summan av två negativa tal - 304 och - 18 007.

Lösning

Låt oss utföra stegen steg för steg. Först måste vi hitta modulerna för talen som adderas: - 304 = 304, - 180007 = 180007. Därefter måste vi utföra tilläggsåtgärden, för vilken vi använder kolumnräkningsmetoden:

Allt som återstår för oss är att sätta ett minus framför resultatet och få - 18 311.

Svar: - - 18 311 .

Vilka tal vi har beror på vad vi kan reducera verkan av addition till: att hitta summan av naturliga tal, lägga till vanliga eller decimala bråk. Låt oss analysera problemet med dessa siffror.

Exempel N

Hitta summan av två negativa tal - 2 5 och − 4, (12).

Lösning

Vi hittar modulerna med de nödvändiga siffrorna och får 2 5 och 4, (12). Vi fick två olika bråk. Låt oss reducera problemet till tillägget av två vanliga bråk, för vilka vi representerar det periodiska bråket i form av ett vanligt:

4 , (12) = 4 + (0 , 12 + 0 , 0012 + . . .) = 4 + 0 , 12 1 - 0 , 01 = 4 + 0 , 12 0 , 99 = 4 + 12 99 = 4 + 4 33 = 136 33

Som ett resultat fick vi ett bråk som är lätt att lägga till med den första ursprungliga termen (om du har glömt hur du korrekt lägger till bråk med olika nämnare, upprepa motsvarande material).

2 5 + 136 33 = 2 33 5 33 + 136 5 33 5 = 66 165 + 680 165 = 764 165 = 4 86 105

Som ett resultat fick vi ett blandat nummer, framför vilket vi bara behöver sätta ett minus. Detta avslutar beräkningarna.

Svar: - 4 86 105 .

Verkliga negativa tal summerar på liknande sätt. Resultatet av en sådan åtgärd skrivs vanligtvis ner som ett numeriskt uttryck. Dess värde får inte beräknas eller begränsas till ungefärliga beräkningar. Så, till exempel, om vi behöver hitta summan - 3 + (− 5), så skriver vi svaret som - 3 − 5. Vi har ägnat ett separat material åt tillägg av reella tal, där du kan hitta andra exempel.

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

Utveckling av beräkningsfärdigheter är det viktigaste målet som eftersträvas av matematikprogram från årskurs 1 till 6. Hur snabbt och korrekt ett barn lär sig att utföra aritmetiska operationer kommer att avgöra hastigheten med vilken han utför logiska (semantiska) operationer i gymnasiet och nivån av förståelse för ämnet som helhet. En matematiklärare stöter ganska ofta på elevers datorproblem som hindrar dem från att uppnå bra resultat.

Vilken typ av elever har en handledare att arbeta med? Föräldrar behöver förbereda sig för Unified State Exam i matematik, men deras barn kan inte förstå vanliga bråktal eller blir förvirrad av negativa tal. Vilka åtgärder bör en matematiklärare vidta i sådana fall? Hur hjälper man en student? Handledaren har inte tid för en lugn och konsekvent studie av reglerna, så traditionella metoder måste ofta ersättas med några konstgjorda "halvfärdiga acceleratorer", så att säga. I den här artikeln kommer jag att beskriva ett av de möjliga sätten att utveckla färdigheten att utföra åtgärder med negativa tal, nämligen att subtrahera dem.

Låt oss anta att en matematiklärare har nöjet att arbeta med en mycket svag elev vars kunskaper inte sträcker sig längre än till de enklaste beräkningarna med positiva tal. Låt oss också anta att handledaren lyckades förklara additionens lagar och komma nära regeln a-b=a+(-b). Vilka punkter bör en matematiklärare ta hänsyn till?

Att reducera subtraktion till addition är inte en enkel och självklar transformation. Läroböcker erbjuder strikta och exakta matematiska formuleringar: "För att subtrahera talet "b" från talet "a", måste du lägga till det motsatta talet till "b" till talet "a". Formellt kan du inte hitta fel på texten, men så fort en matematiklärare börjar använda den som instruktioner för att utföra specifika beräkningar, uppstår problem. Bara frasen är värt det: "För att subtrahera måste du lägga till." Utan en tydlig kommentar från handledaren kommer eleven inte att förstå. Vad ska du faktiskt göra: subtrahera eller addera?

Om du arbetar med regeln enligt avsikten från författarna till läroboken, måste du förutom att öva begreppet "motsatt nummer", lära studenten att relatera beteckningarna "a" och "b" till det verkliga siffror i exemplet. Och detta kommer att ta tid. Med tanke på det faktum att eleven tänker och skriver samtidigt, blir uppgiften som en mattelärare ännu mer komplicerad. En svag elev har inte bra visuellt, semantiskt och motoriskt minne, och därför är det bättre att erbjuda en alternativ text av regeln:

För att subtrahera den andra från den första siffran behöver du
A) Skriv om den första siffran
B) Sätt ett plus
B) Byt ut tecknet för den andra siffran mot den motsatta
D) Lägg till de resulterande talen

Här är stegen i algoritmen tydligt indelade i punkter och är inte bundna till bokstavsbeteckningar.

I samband med att lösa en praktisk uppgift om översättningar, läser matematikläraren om denna text för eleven flera gånger (för memorering). Jag råder dig att skriva ner det i din teoretiska anteckningsbok. Först efter att ha utarbetat regeln för övergång till addition kan du skriva ner den allmänna formen a-b=a+(-b)

Rörelsen av minus- och plustecknen i huvudet på ett barn (både en liten och en svag vuxen) påminner något om Brownian. Matematikläraren måste få ordning på detta kaos så snabbt som möjligt. I processen att lösa exempel används stödjande ledtrådar (verbala och visuella), som i kombination med snygg och detaljerad formatering gör sitt jobb. Man måste komma ihåg att varje ord som uttalas av en matematiklärare i ögonblicket för att lösa ett problem har antingen en antydan eller ett hinder. Varje fras analyseras av barnet för att upprätta ett samband med ett eller annat matematiskt objekt (fenomen) och dess bild på papper.

Ett typiskt problem för svaga skolbarn är att separera tecknet på en handling från tecknet på antalet som är involverat i den. Samma visuella bild gör det svårt att känna igen minuenden "a" och det subtraherade "b" i a-b-skillnaden. När en matematiklärare läser ett uttryck under en förklaring måste du se till att istället för "-" används ordet "subtrahera". Det är nödvändigt! Till exempel bör inlägget lyda: ”Ut av minus fem subtrahera minus tre." Vi får inte glömma regeln om översättning till addition: "Så att från siffran "a" subtrahera siffran "b" är nödvändig..."

Om en mattehandledare hela tiden säger "minus 5 minus minus 3", så är det klart att det blir svårare för eleven att föreställa sig exemplets struktur. En en-till-en-överensstämmelse mellan ett ord och en aritmetisk operation hjälper en matematiklärare att förmedla information korrekt.

Hur kan en handledare förklara övergången till addition?

Naturligtvis kan du hänvisa till definitionen av "subtrahera" och leta efter talet som måste läggas till "b" för att få "a". Men en svag elev tänker långt ifrån strikt matematik och handledaren kommer att behöva några analogier med enkla handlingar när han arbetar med honom. Jag säger ofta till mina sjätteklassare: "I matematik finns det ingen sådan aritmetisk operation som skillnad." Notationen 5 – 3 är en enkel notation för resultatet av addition 5+(-3). Plustecknet utelämnas helt enkelt och skrivs inte."

Barn blir förvånade över handledarens ord och kommer ofrivilligt ihåg att de inte kan subtrahera siffror direkt. Matematikläraren deklarerar 5 och -3 termer, och för att göra hans ord mer övertygande, jämför resultaten av åtgärderna 5-3 och 5+(-3). Efter detta skrivs identiteten a-b=a+(-b).

Oavsett vilken typ av elev, och oavsett hur mycket tid matematikläraren har på sig att arbeta med honom, måste du räkna ut begreppet "motsatt nummer" i tid. Posten "-x" förtjänar särskild uppmärksamhet från en matematiklärare. En elev i 6:e klass måste lära sig att det inte representerar ett negativt tal, utan motsatsen till X.

Det är nödvändigt att uppehålla sig separat vid beräkningar med två minustecken som ligger bredvid varandra. Problemet uppstår med att förstå hur de samtidigt avlägsnas. Du måste noggrant gå igenom alla punkter i den skisserade algoritmen för övergång till addition. Det blir bättre om matematikläraren, när man arbetar med skillnaden -5- (-3), innan de gör några kommentarer, markerar siffrorna -5 och -3 i en ram eller understryker dem. Detta kommer att hjälpa eleven att identifiera komponenterna i åtgärden.

Mattelärarens fokus på memorering

Tillförlitlig memorering är resultatet av den praktiska tillämpningen av matematiska regler, så det är viktigt för handledaren att säkerställa en god täthet av självständigt lösta exempel. För att förbättra stabiliteten i memoreringen kan du ringa efter hjälp med visuella signaler - chips. Till exempel ett intressant sätt att omvandla subtraktionen av ett negativt tal till addition. Matematikläraren kopplar ihop två minus med en linje (som visas i figuren), och elevens blick öppnar sig för ett plustecken (vid skärningspunkten med fästet).

För att förhindra distraktion rekommenderar jag att mattelärare markerar minuend och subtrahend med rutor. Om en matematiklärare använder ramar eller cirklar för att markera komponenterna i en aritmetisk operation, kommer eleven att lättare och snabbare kunna se exemplets struktur och relatera det till motsvarande regel. När du ritar upp lösningar bör du inte placera delar av hela objektet på olika rader av ett anteckningsblock och även börja lägga till tills det är nedskrivet. Alla åtgärder och övergångar visas nödvändigtvis (åtminstone i början av att studera ämnet).

Vissa matematiklärare strävar efter 100 % korrekt motivering av översättningsregler, och anser att denna strategi är den enda korrekta och användbara för att utveckla beräkningsfärdigheter. Praxis visar dock att denna väg inte alltid ger bra utdelning. Behovet av att förstå vad en person gör uppstår oftast efter att ha memorerat stadierna i den använda algoritmen och praktisk konsolidering av beräkningsoperationer.

Det är oerhört viktigt att öva på övergången till en summa i ett långt numeriskt uttryck med flera subtraktioner, till exempel. Innan jag räknar eller räknar om låter jag eleven ringa in siffrorna tillsammans med deras tecken till vänster. Bilden visar ett exempel på hur en matematiklärare identifierar termer För mycket svaga sjätteklassare kan du dessutom färga cirklarna. Använd en färg för positiva termer och en annan färg för negativa termer. Vid speciella tillfällen tar jag upp en sax och skär uttrycket i bitar. De kan omarrangeras godtyckligt, vilket simulerar omarrangemanget av termer. Barnet kommer att se att tecknen rör sig tillsammans med själva termerna. Det vill säga, om minustecknet var till vänster om siffran 5, så kommer det inte att lossna från femman, oavsett var vi flyttar motsvarande kort.

Kolpakov A.N. Matematiklärare för årskurs 5-6. Moskva. Strogino.

I den här artikeln kommer vi att prata om lägga till negativa tal. Först ger vi regeln för att addera negativa tal och bevisar det. Efter detta ska vi titta på typiska exempel på att lägga till negativa tal.

Sidnavigering.

Innan vi formulerar regeln för att lägga till negativa tal, låt oss vända oss till materialet i artikeln: positiva och negativa tal. Där nämnde vi att negativa tal kan uppfattas som skuld, och modulen för talet i detta fall avgör storleken på denna skuld. Därför är tillägget av två negativa tal tillägget av två skulder.

Denna slutsats låter oss inse regel för att lägga till negativa tal. För att lägga till två negativa tal behöver du:

• vika sina moduler;
• sätt ett minustecken framför det mottagna beloppet.

Låt oss skriva ner regeln för att lägga till negativa tal −a och −b i bokstavsform: (−a)+(−b)=−(a+b) .

Det är tydligt att den angivna regeln reducerar additionen av negativa tal till additionen av positiva tal (modulen för ett negativt tal är ett positivt tal). Det är också tydligt att resultatet av att lägga till två negativa tal är ett negativt tal, vilket framgår av minustecknet som är placerat framför summan av modulerna.

Regeln för att lägga till negativa tal kan bevisas utifrån egenskaper för operationer med reella tal(eller samma egenskaper för operationer med rationella eller heltal). För att göra detta räcker det att visa att skillnaden mellan vänster och höger sida av likheten (−a)+(−b)=−(a+b) är lika med noll.

Eftersom att subtrahera ett tal är detsamma som att addera det motsatta talet (se regeln för att subtrahera heltal), då (−a)+(−b)−(−(a+b))=(−a)+(−b) +(a+b). På grund av additionens kommutativa och kombinativa egenskaper har vi (−a)+(−b)+(a+b)=(−a+a)+(−b+b) . Eftersom summan av motsatta tal är lika med noll, då (−a+a)+(−b+b)=0+0 och 0+0=0 på grund av egenskapen att addera ett tal med noll. Detta bevisar likheten (−a)+(−b)=−(a+b) , och därav regeln för att addera negativa tal.

Denna additionsregel gäller alltså både negativa heltal och rationella tal, såväl som reella tal.

Allt som återstår är att lära sig hur man tillämpar regeln att lägga till negativa tal i praktiken, vilket vi kommer att göra i nästa stycke.

Exempel på att lägga till negativa tal

Låt oss reda ut det exempel på att lägga till negativa tal. Låt oss börja med det enklaste fallet - tillägget av negativa heltal kommer vi att utföra tillägget enligt regeln som diskuterades i föregående stycke.

Lägg till de negativa talen -304 och -18 007.

Låt oss följa alla steg i regeln för att lägga till negativa tal.

Först hittar vi modulerna för de siffror som läggs till: och . Nu måste du lägga till de resulterande siffrorna här är det bekvämt att utföra kolumntillägg:

Nu sätter vi ett minustecken framför det resulterande talet, som ett resultat har vi −18,311.

Låt oss skriva hela lösningen i en kort form: (−304)+(−18,007)= −(304+18,007)=−18,311.

Tillägget av negativa rationella tal, beroende på talen i sig, kan reduceras antingen till tillägg av naturliga tal, eller till tillägg av vanliga bråk eller till tillägg av decimalbråk.

Lägg till ett negativt tal och ett negativt tal −4,(12) .

Enligt regeln för att lägga till negativa tal måste du först beräkna summan av modulerna. Modulerna för de negativa talen som adderas är lika med 2/5 respektive 4, (12). Adderingen av de resulterande talen kan reduceras till additionen av vanliga bråk. För att göra detta omvandlar vi det periodiska decimalbråket till ett vanligt bråktal: . Således, 2/5+4,(12)=2/5+136/33. Låt oss nu lägga till bråk med olika nämnare: .

Allt som återstår är att sätta ett minustecken framför det resulterande talet: . Detta avslutar tillägget av de ursprungliga negativa talen.

Genom att använda samma regel för att lägga till negativa tal läggs även negativa reella tal till. Det är värt att notera här att resultatet av att lägga till reella tal mycket ofta skrivs i form av ett numeriskt uttryck, och värdet av detta uttryck beräknas ungefär, och då endast om det behövs.

Låt oss till exempel hitta summan av negativa tal och −5. Modulerna för dessa tal är lika med kvadratroten av tre respektive fem, och summan av de ursprungliga talen är lika med . Så här är svaret skrivet. Andra exempel finns i artikeln addition av reella tal.

www.cleverstudents.ru

Regeln för att lägga till två negativa tal

Åtgärder med negativa och positiva siffror

Absolut värde (modul). Tillägg.

Subtraktion. Multiplikation. Division.

Absolut värde (modul). För negativt tal– är ett positivt tal som erhålls genom att ändra dess tecken från “–” till “+”; För Positivt nummer och noll– det här är själva numret. För att ange absolutvärdet (modulen) för ett tal används två raka linjer, inom vilka detta tal skrivs.

EXEMPEL: | – 5 | = 5, | 7 | = 7, | 0 | = 0.

1) När två siffror med samma tecken adderas, summeras de

deras absoluta värden och ett vanligt tecken placeras framför summan.

2) När man lägger till två tal med olika tecken är deras absoluta värden

kvantiteter subtraheras (från de större mindre) och tecknet sätts

tal med ett större absolutvärde.

Subtraktion. Du kan ersätta subtraktionen av två tal med addition, där minuenden behåller sitt tecken, och subtrahenden tas med motsatt tecken.

(+ 8) – (+ 5) = (+ 8) + (– 5) = 3;

(+ 8) – (– 5) = (+ 8) + (+ 5) = 13;

(– 8) – (– 5) = (– 8) + (+ 5) = – 3;

(– 8) – (+ 5) = (– 8) + (– 5) = – 13;

Multiplikation. När två tal multipliceras multipliceras deras absoluta värden, och produkten antar tecknet "+" om tecknen på faktorerna är desamma och tecknet "–" om tecknen på faktorerna är olika.

Följande diagram är användbart ( multiplikationsteckenregler):

När du multiplicerar flera tal (två eller fler) har produkten ett "+"-tecken om antalet negativa faktorer är jämnt och ett "–"-tecken om deras tal är udda.

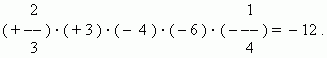
Division. När man dividerar två tal divideras det absoluta värdet av utdelningen med det absoluta värdet av divisorn, och kvoten tar "+"-tecknet om tecknen för utdelningen och divisorn är samma, och "–"-tecknet om tecken på utdelning och divisor är olika.

Agera här Det samma teckenreglerna är desamma som för multiplikation:

Lägga till negativa tal

Addering av positiva och negativa tal kan analyseras med hjälp av nummeraxeln.

Lägga till tal med hjälp av en koordinatlinje

Det är bekvämt att lägga till små modultal på en koordinatlinje och mentalt föreställa sig hur punkten som betecknar talet rör sig längs talaxeln.

Låt oss ta ett antal, till exempel 3. Låt oss beteckna det på talaxeln med punkten "A".

Låt oss lägga till det positiva talet 2 till talet. Detta innebär att punkt "A" måste flyttas två enhetssegment i positiv riktning, det vill säga åt höger. Som ett resultat får vi punkt "B" med koordinat 5.

För att lägga till det negativa talet "−5" till ett positivt tal, till exempel till 3, måste punkt "A" flyttas 5 längdenheter i negativ riktning, det vill säga åt vänster.

I detta fall är koordinaten för punkt "B" lika med "2".

Så ordningen för att lägga till rationella tal med hjälp av tallinjen kommer att vara följande:

markera punkten "A" på koordinatlinjen med en koordinat lika med den första termen;

flytta det ett avstånd lika med modulen för den andra termen i den riktning som motsvarar tecknet framför det andra numret (plus - flytta till höger, minus - till vänster);

punkten "B" som erhålls på axeln kommer att ha en koordinat som kommer att vara lika med summan av dessa tal.

När vi flyttar från punkt - 2 till vänster (eftersom det finns ett minustecken framför 6) får vi - 8.

Lägga till siffror med samma tecken

Att lägga till rationella tal kan vara lättare om du använder begreppet modul.

Låt oss behöva lägga till siffror som har samma tecken.

För att göra detta kasserar vi siffrornas tecken och tar modulerna för dessa siffror. Låt oss lägga till modulerna och sätta tecknet framför summan som var gemensam för dessa siffror.

Ett exempel på att lägga till negativa tal.

För att lägga till siffror av samma tecken måste du lägga till deras moduler och framför summan sätta tecknet som var före termerna.

Lägga till siffror med olika tecken

Om siffrorna har olika tecken, agerar vi något annorlunda än när vi lägger till siffror med samma tecken.

Vi kasserar tecknen framför siffrorna, det vill säga vi tar deras moduler.

Från den större modulen subtraherar vi den mindre.

Innan skillnaden satte vi tecknet som var för numret med en större modul.

Exempel på att lägga till ett negativt och ett positivt tal.

Ett exempel på att lägga till blandade tal.

Till lägga till antal olika tecken nödvändig:

• subtrahera den mindre modulen från den större modulen;
• Före den resulterande skillnaden, sätt tecknet för talet med den större modulen.

Addera och subtrahera positiva och negativa tal

Kan inte förstå någonting?

Försök att be dina lärare om hjälp

Regel för att lägga till negativa tal

För att lägga till två negativa tal behöver du:

• utföra tillägg av sina moduler;
• lägg till ett "–"-tecken till det mottagna beloppet.

Enligt additionsregeln kan vi skriva:

Regeln för att lägga till negativa tal gäller negativa heltal, rationella tal och reella tal.

Lägg till de negativa talen $−185$ och $−23\789.$

Låt oss använda regeln för att lägga till negativa tal.

Låt oss lägga till de resulterande siffrorna:

$185+23 \ 789=23 \ 974$.

Sätt $“–”$-tecknet framför det hittade numret och få $−23,974$.

Kort lösning: $(−185)+(−23\789)=−(185+23\789)=−23\974$.

När negativa rationella tal adderas måste de omvandlas till formen av naturliga tal, vanliga eller decimala bråk.

Lägg till de negativa talen $-\frac $ och $−7.15$.

Enligt regeln för att lägga till negativa tal måste du först hitta summan av modulerna:

Det är bekvämt att reducera de erhållna värdena till decimalbråk och utföra deras addition:

Låt oss sätta $“–”$-tecknet framför det resulterande värdet och få $–7,4$.

Kort sammanfattning av lösningen:

Lägga till siffror med motsatta tecken

Regel för att lägga till tal med motsatta tecken:

• beräkna modulerna av siffror;
• jämför de resulterande siffrorna:

om de är lika, då är de ursprungliga talen motsatta och deras summa är noll;

om de inte är lika, måste du komma ihåg tecknet för talet vars modul är större;

• subtrahera den mindre från den större modulen;
• Före det resulterande värdet, sätt tecknet för det tal vars modul är större.

Att lägga till tal med motsatta tecken innebär att man subtraherar ett mindre negativt tal från ett större positivt tal.

Regeln för att lägga till tal med motsatta tecken gäller heltal, rationaler och reella tal.

Lägg till siffrorna $4$ och $−8$.

Du måste lägga till siffror med motsatta tecken. Låt oss använda motsvarande additionsregel.

Låt oss hitta modulerna för dessa siffror:

Modulen för talet $−8$ är större än modulen för talet $4$, dvs. kom ihåg $“–”$-tecknet.

Låt oss sätta $“–”$-tecknet, som vi kom ihåg, framför det resulterande talet, och vi får $−4.$

För lat för att läsa?

Ställ en fråga till experterna och få
svar inom 15 minuter!

För att lägga till rationella tal med motsatta tecken är det lämpligt att representera dem i form av vanliga eller decimala bråk.

Subtrahera negativa tal

Regel för att subtrahera negativa tal:

För att subtrahera ett negativt tal $b$ från ett tal $a$, är det nödvändigt att lägga till talet $−b$ till minuenden $a$, vilket är motsatsen till subtrahenden $b$.

Enligt subtraktionsregeln kan vi skriva:

Denna regel är giltig för heltal, rationaler och reella tal. Regeln kan användas för att subtrahera ett negativt tal från ett positivt tal, från ett negativt tal och från noll.

Subtrahera det negativa talet $−5$ från det negativa talet $−28$.

Det motsatta talet för talet $–5$ är talet $5$.

Enligt regeln för att subtrahera negativa tal får vi:

Låt oss lägga till siffror med motsatta tecken:

Kort lösning: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.

När du subtraherar negativa bråk, måste du konvertera talen till bråk, blandade tal eller decimaler.

Subtrahera siffror med motsatta tecken

Regeln för att subtrahera tal med motsatta tecken är densamma som regeln för att subtrahera negativa tal.

Subtrahera det positiva talet $7$ från det negativa talet $−11$.

Motsatsen till $7$ är $–7$.

Enligt regeln för att subtrahera tal med motsatta tecken får vi:

Låt oss lägga till negativa tal:

När du subtraherar bråktal med motsatta tecken, är det nödvändigt att konvertera talen till formen av vanliga eller decimala bråk.

Hittade aldrig svaret
på din fråga?

Skriv bara vad du behöver
hjälp behövs

Tillägg av negativa tal: regel, exempel

I det här materialet kommer vi att beröra ett så viktigt ämne som att lägga till negativa siffror. I det första stycket kommer vi att berätta den grundläggande regeln för denna åtgärd, och i det andra kommer vi att titta på specifika exempel på att lösa sådana problem.

Grundregel för att lägga till naturliga tal

Innan vi härleder regeln, låt oss komma ihåg vad vi generellt vet om positiva och negativa tal. Tidigare var vi överens om att negativa tal ska uppfattas som skuld, förlust. Modulen för ett negativt tal uttrycker den exakta storleken på denna förlust. Då kan tillägget av negativa tal representeras som ett tillägg av två förluster.

Med hjälp av detta resonemang formulerar vi grundregeln för att lägga till negativa tal.

För att slutföra lägga till negativa tal, måste du lägga ihop värdena för deras moduler och sätta ett minus framför resultatet. I bokstavlig form ser formeln ut som (− a) + (− b) = − (a + b) .

Baserat på denna regel kan vi dra slutsatsen att att lägga till negativa tal liknar att lägga till positiva, bara i slutändan måste vi få ett negativt tal, eftersom vi måste sätta ett minustecken framför summan av modulerna.

Vilka bevis kan ges för denna regel? För att göra detta måste vi komma ihåg de grundläggande egenskaperna för operationer med reella tal (eller med heltal eller med rationella tal - de är samma för alla dessa typer av tal). För att bevisa det behöver vi bara visa att skillnaden mellan vänster och höger sida av likheten (− a) + (− b) = − (a + b) kommer att vara lika med 0.

Att subtrahera ett tal från ett annat är detsamma som att lägga till samma motsatta tal till det. Därför, (− a) + (− b) − (− (a + b)) = (− a) + (− b) + (a + b) . Kom ihåg att numeriska uttryck med addition har två huvudegenskaper - associativa och kommutativa. Då kan vi dra slutsatsen att (− a) + (− b) + (a + b) = (− a + a) + (− b + b) . Eftersom vi, genom att lägga till motsatta tal, alltid får 0, då (− a + a) + (− b + b) = 0 + 0, och 0 + 0 = 0. Vår likhet kan anses bevisad, vilket betyder att regeln för lägga till negativa tal Vi bevisade det också.

Problem med att lägga till negativa tal

I det andra stycket kommer vi att ta specifika problem där vi behöver lägga till negativa tal, och vi kommer att försöka tillämpa den inlärda regeln på dem.

Hitta summan av två negativa tal - 304 och - 18 007.

Lösning

Låt oss utföra stegen steg för steg. Först måste vi hitta modulerna för talen som adderas: - 304 = 304, - 180007 = 180007. Därefter måste vi utföra tilläggsåtgärden, för vilken vi använder kolumnräkningsmetoden:



Allt vi har kvar är att sätta ett minus framför resultatet och få - 18 311.

Svar: — — 18 311 .

Vilka tal vi har beror på vad vi kan reducera verkan av addition till: att hitta summan av naturliga tal, lägga till vanliga eller decimala bråk. Låt oss analysera problemet med dessa siffror.

Hitta summan av två negativa tal - 2 5 och − 4, (12).

Vi hittar modulerna med de nödvändiga siffrorna och får 2 5 och 4, (12). Vi fick två olika bråk. Låt oss reducera problemet till tillägget av två vanliga bråk, för vilka vi representerar det periodiska bråket i form av ett vanligt:

4 , (12) = 4 + (0 , 12 + 0 , 0012 + . . .) = 4 + 0 , 12 1 — 0 , 01 = 4 + 0 , 12 0 , 99 = 4 + 12 99 = 4 + 4 33 = 136 33

Som ett resultat fick vi ett bråk som är lätt att lägga till med den första ursprungliga termen (om du har glömt hur du korrekt lägger till bråk med olika nämnare, upprepa motsvarande material).

2 5 + 136 33 = 2 33 5 33 + 136 5 33 5 = 66 165 + 680 165 = 764 165 = 4 86 105

Som ett resultat fick vi ett blandat nummer, framför vilket vi bara behöver sätta ett minus. Detta avslutar beräkningarna.

Svar: — 4 86 105 .

Verkliga negativa tal summerar på liknande sätt. Resultatet av en sådan åtgärd skrivs vanligtvis ner som ett numeriskt uttryck. Dess värde får inte beräknas eller begränsas till ungefärliga beräkningar. Så, till exempel, om vi behöver hitta summan - 3 + (− 5), så skriver vi svaret som - 3 − 5. Vi har ägnat ett separat material åt tillägg av reella tal, där du kan hitta andra exempel.

Låt oss börja med ett enkelt exempel. Låt oss bestämma vad uttrycket 2-5 är lika med. Från punkt +2 kommer vi att lägga ner fem divisioner, två till noll och tre under noll. Låt oss stanna vid punkt -3. Det vill säga 2-5=-3. Lägg nu märke till att 2-5 inte alls är lika med 5-2. Om deras ordning inte spelar någon roll när det gäller att lägga till tal, så är allt annorlunda när det gäller subtraktion. Ordningen på siffrorna spelar roll.

Nu ska vi gå till negativt område vågar. Anta att vi behöver lägga till +5 till -2. (Från och med nu kommer vi att sätta "+"-tecken framför positiva tal och sätta både positiva och negativa tal inom parentes för att inte förväxla tecknen framför siffror med additions- och subtraktionstecken.) Nu kan vårt problem skrivas som (-2)+ (+5). För att lösa det går vi upp fem divisioner från punkt -2 och hamnar på punkt +3.

Finns det någon praktisk mening med denna uppgift? Har såklart. Låt oss säga att du har $2 i skuld och att du tjänade $5. På så sätt, efter att du har betalat av skulden, kommer du att ha $3 kvar.

Du kan också flytta ned det negativa området på skalan. Anta att du behöver subtrahera 5 från -2, eller (-2)-(+5). Från punkt -2 på skalan, flytta ner fem divisioner och hamna på punkt -7. Vad är den praktiska innebörden av denna uppgift? Låt oss säga att du hade en skuld på $2 och var tvungen att låna ytterligare $5. Din skuld är nu $7.

Vi ser att med negativa tal kan vi utföra samma sak additions- och subtraktionsoperationer, som med de positiva.

Det är sant att vi ännu inte bemästrat alla operationer. Vi adderade bara till negativa tal och subtraherade endast positiva från negativa tal. Vad ska du göra om du behöver lägga till negativa tal eller subtrahera negativa tal från negativa tal?

I praktiken liknar detta skuldtransaktioner. Låt oss säga att du debiterades $5 i skuld, det betyder samma sak som om du fick $5. Å andra sidan, om jag på något sätt tvingar dig att ta ansvar för någon annans skuld på $5, skulle det vara samma sak som att ta de $5 ifrån dig. Det vill säga att subtrahera -5 är detsamma som att addera +5. Och att lägga till -5 är detsamma som att subtrahera +5.

Detta gör att vi kan bli av med subtraktionsoperationen. "5-2" är faktiskt detsamma som (+5)-(+2) eller enligt vår regel (+5)+(-2). I båda fallen får vi samma resultat. Från punkt +5 på skalan behöver vi gå ner två divisioner och vi får +3. I fallet med 5-2 är detta uppenbart, eftersom subtraktion är en nedåtgående rörelse.

I fallet med (+5)+(-2) är detta mindre uppenbart. Vi adderar ett tal, vilket betyder att vi flyttar uppåt på skalan, men vi lägger till ett negativt tal, vilket betyder att vi gör tvärtom, och dessa två faktorer tillsammans gör att vi inte behöver flytta uppåt på skalan, utan tvärtom. riktning, det vill säga ner.

Således får vi återigen svaret +3.

Varför är det nödvändigt egentligen? ersätt subtraktion med addition? Varför gå upp "i motsatt mening"? Är det inte lättare att bara flytta ner? Anledningen är att vid addition spelar ordningen på termerna ingen roll, men vid subtraktion är det väldigt viktigt.

Vi har redan tidigare upptäckt att (+5)-(+2) inte alls är detsamma som (+2)-(+5). I det första fallet är svaret +3 och i det andra -3. Å andra sidan resulterar (-2)+(+5) och (+5)+(-2) i +3. Genom att byta till addition och överge subtraktionsoperationer kan vi alltså undvika slumpmässiga fel associerade med omarrangering av addends.

Du kan göra detsamma när du subtraherar ett negativt. (+5)-(-2) är samma som (+5)+(+2). I båda fallen får vi svaret +7. Vi börjar vid punkt +5 och rör oss "nedåt i motsatt riktning", det vill säga uppåt. Vi skulle agera på exakt samma sätt när vi löser uttrycket (+5)+(+2).

Elever använder aktivt att ersätta subtraktion med addition när de börjar studera algebra, och därför kallas denna operation "algebraisk tillägg". Detta är faktiskt inte helt rättvist, eftersom en sådan operation uppenbarligen är aritmetisk och inte alls algebraisk.

Denna kunskap är oförändrad för alla, så även om du får utbildning i Österrike via www.salls.ru, även om studier utomlands värderas högre, kommer du att kunna tillämpa dessa regler även där.

Nästan hela matematikkursen bygger på operationer med positiva och negativa tal. När allt kommer omkring, så snart vi börjar studera koordinatlinjen, börjar siffror med plus- och minustecken dyka upp överallt, i varje nytt ämne. Det finns inget lättare än att lägga ihop vanliga positiva tal, det är inte svårt att subtrahera det ena från det andra. Även aritmetik med två negativa tal är sällan ett problem.

Men många människor blir förvirrade när det gäller att lägga till och subtrahera tal med olika tecken. Låt oss komma ihåg reglerna för dessa åtgärder.

Lägga till siffror med olika tecken

Om vi ​​för att lösa ett problem måste lägga till ett negativt tal "-b" till något tal "a", måste vi agera enligt följande.

• Låt oss ta modulerna för båda talen - |a| och |b| - och jämför dessa absoluta värden med varandra.
• Låt oss notera vilken modul som är större och vilken som är mindre, och subtrahera det mindre värdet från det större värdet.
• Låt oss sätta före det resulterande talet tecknet för det tal vars modul är större.

Detta kommer att vara svaret. Vi kan uttrycka det enklare: om i uttrycket a + (-b) modulen för talet "b" är större än modulen för "a", så subtraherar vi "a" från "b" och sätter ett "minus" ” framför resultatet. Om modulen "a" är större, subtraheras "b" från "a" - och lösningen erhålls med ett "plus"-tecken.

Det händer också att modulerna visar sig vara lika. Om så är fallet kan vi sluta vid denna punkt - vi talar om motsatta tal, och deras summa kommer alltid att vara lika med noll.

Subtrahera siffror med olika tecken

Vi har behandlat addition, låt oss nu titta på regeln för subtraktion. Det är också ganska enkelt - och dessutom upprepar det helt en liknande regel för att subtrahera två negativa tal.

För att subtrahera från ett visst tal "a" - godtyckligt, det vill säga med vilket tecken som helst - ett negativt tal "c", måste du lägga till vårt godtyckliga tal "a" talet mitt emot "c". Till exempel:

• Om "a" är ett positivt tal och "c" är negativt, och du måste subtrahera "c" från "a", så skriver vi det så här: a – (-c) = a + c.
• Om "a" är ett negativt tal och "c" är positivt och "c" måste subtraheras från "a", så skriver vi det så här: (- a)– c = - a+ (-c).

Sålunda, när vi subtraherar tal med olika tecken, återgår vi till reglerna för addition, och när vi adderar tal med olika tecken, återgår vi till reglerna för subtraktion. Genom att memorera dessa regler kan du lösa problem snabbt och enkelt.