Okresowy ułamek dziesiętny. Posty oznaczone "jak zapisać liczbę w postaci ułamka dziesiętnego nieskończenie okresowego"

Ułamek okresowy

nieskończony ułamek dziesiętny, w którym począwszy od pewnego miejsca występuje tylko okresowo powtarzana pewna grupa cyfr. Na przykład 1,3181818...; Krótko mówiąc, ułamek ten zapisuje się w ten sposób: 1,3(18), to znaczy umieszcza się kropkę w nawiasie (i mówi: „18 w kropce”). P. nazywa się czystym, jeśli kropka rozpoczyna się bezpośrednio po przecinku, np. 2(71) = 2,7171..., i mieszanym, jeśli po przecinku znajdują się liczby poprzedzające kropkę, np. 1,3(18). Rola ułamków dziesiętnych w arytmetyce wynika z faktu, że gdy liczby wymierne, czyli ułamki zwyczajne (proste), są reprezentowane przez ułamki dziesiętne, zawsze otrzymuje się ułamki skończone lub okresowe. Dokładniej: końcowy ułamek dziesiętny otrzymuje się wtedy, gdy w mianowniku nieredukowalnego ułamka prostego nie znajdują się inne czynniki pierwsze niż 2 i 5; we wszystkich pozostałych przypadkach wynikiem jest ułamek P., a ponadto jest czysty, jeśli mianownik danego ułamka nieredukowalnego w ogóle nie zawiera współczynników 2 i 5, i mieszany, jeśli zawiera się przynajmniej jeden z tych współczynników w mianowniku. Dowolny ułamek ułamkowy można zamienić na ułamek prosty (to znaczy jest równy jakiejś liczbie wymiernej). Ułamek czysty to ułamek prosty, którego licznikiem jest kropka, a mianownikiem jest liczba 9, zapisana tyle razy, ile jest cyfr w tym okresie; Przy zamianie ułamka mieszanego na ułamek prosty licznikiem jest różnica między liczbą reprezentowaną przez liczby poprzedzające drugi kropkę a liczbą reprezentowaną przez liczby poprzedzające pierwszy kropkę; Aby utworzyć mianownik, należy wpisać liczbę 9 tyle razy, ile jest liczb w danym okresie, i dodać po prawej stronie tyle zer, ile jest liczb przed kropką. Reguły te zakładają, że dane P. jest poprawne, czyli nie zawiera całych jednostek; w przeciwnym razie cała część jest traktowana ze szczególną uwagą.

Znane są również zasady wyznaczania długości okresu ułamka odpowiadającego danemu ułamkowi zwykłemu. Na przykład dla ułamka a/str, Gdzie R - liczba pierwsza i 1 ≤ A ≤ P- 1, długość okresu jest dzielnikiem R - 1. Zatem w przypadku znanych przybliżeń liczby (patrz Pi) Okresy 22/7 i 355/113 są równe odpowiednio 6 i 112.

Wielka encyklopedia radziecka. - M .: Encyklopedia radziecka. 1969-1978 .

Synonimy:

Zobacz, co oznacza „Ułamek okresowy” w innych słownikach:

Nieskończony ułamek dziesiętny, w którym rozpoczynając od określonego miejsca, okresowo powtarza się np. pewna grupa cyfr (kropka). 0,373737... czysta frakcja okresowa lub 0,253737... mieszana frakcja okresowa... Wielki słownik encyklopedyczny

Ułamek, ułamek nieskończony Słownik rosyjskich synonimów. rzeczownik ułamkowy okresowy, liczba synonimów: 2 ułamek nieskończony (2) ... Słownik synonimów

Ułamek dziesiętny, w którym ciąg cyfr powtarza się w tej samej kolejności. Na przykład 0,135135135... to p.d., którego okres wynosi 135 i który jest równy ułamkowi prostemu 135/999 = 5/37. Słownik słów obcych zawartych w języku rosyjskim. Pawlenkow F... Słownik obcych słów języka rosyjskiego

Ułamek dziesiętny to ułamek zwykły o mianowniku 10n, gdzie n jest liczbą naturalną. Ma specjalną formę zapisu: część całkowita w systemie dziesiętnym, następnie przecinek, a następnie część ułamkowa w systemie dziesiętnym oraz liczba cyfr części ułamkowej ... Wikipedia

Nieskończony ułamek dziesiętny, w którym począwszy od pewnego miejsca okresowo powtarza się pewna grupa cyfr (kropka); na przykład 0,373737... czysta frakcja okresowa lub 0,253737... mieszana frakcja okresowa. * * * OKRESOWE… … słownik encyklopedyczny

Nieskończony ułamek dziesiętny, w którym począwszy od określonego miejsca definicja jest okresowo powtarzana. grupa cyfr (kropka); na przykład 0,373737... czysty P. d. lub 0,253737... mieszany P. d. ... Historia naturalna. słownik encyklopedyczny

Zobacz część... Słownik rosyjskich synonimów i podobnych wyrażeń. pod. wyd. N. Abramova, M.: Russian Dictionaries, 1999. ułamek drobiazg, część; dunst, piłka, posiłek, śrut; liczba ułamkowa Słownik rosyjskich synonimów ... Słownik synonimów

okresowe dziesiętne- - [L.G. Sumenko. Słownik angielsko-rosyjski dotyczący technologii informatycznych. M.: Przedsiębiorstwo Państwowe TsNIIS, 2003.] Tematy technologia informacyjna ogólnie EN krążący dziesiętny powtarzający się dziesiętny dziesiętny okresowy dziesiętny okresowy dziesiętny okresowy dziesiętny ... Przewodnik tłumacza technicznego

Jeśli jakaś liczba całkowita a zostanie podzielona przez inną liczbę całkowitą b, czyli poszukiwana będzie liczba x spełniająca warunek bx = a, to mogą zaistnieć dwa przypadki: albo w szeregu liczb całkowitych znajdzie się liczba x spełniająca ten warunek, albo okazało się ,... ... Słownik encyklopedyczny F.A. Brockhausa i I.A. Efrona

Ułamek, którego mianownikiem jest potęga liczby całkowitej 10. Ułamki zwykłe zapisuje się bez mianownika, oddzielając przecinkiem po prawej stronie licznika tyle cyfr, ile jest zer w mianowniku. Na przykład w takim zapisie część po lewej stronie... ... Wielka encyklopedia radziecka

Nieskończone ułamki dziesiętne

Miejsca dziesiętne po przecinku mogą zawierać nieskończoną liczbę cyfr.

Nieskończone ułamki dziesiętne- są to ułamki dziesiętne, które zawierają nieskończoną liczbę cyfr.

Całkowite zapisanie nieskończonego ułamka dziesiętnego jest prawie niemożliwe, dlatego podczas ich zapisywania ograniczają się tylko do określonej skończonej liczby cyfr po przecinku, po czym wstawiają wielokropek, który wskazuje na nieskończenie ciągłą sekwencję cyfr.

Przykład 1

Na przykład $0,443340831\dots ; 3,1415935432\dots ; 135,126730405\kropek ; 4,33333333333\kropki ; 676,68349349\kropki$.

Spójrzmy na dwa ostatnie nieskończone miejsca po przecinku. W ułamku $4,33333333333\dots$ cyfra 3$ powtarza się w nieskończoność, a we ułamku $676,68349349\dots$ grupa cyfr $3$, $4$ i $9$ powtarza się od trzeciego miejsca po przecinku. Takie nieskończone ułamki dziesiętne nazywane są okresowymi.

Okresowe ułamki dziesiętne

Okresowe ułamki dziesiętne(Lub frakcje okresowe) to nieskończone ułamki dziesiętne, przy zapisie których pewna liczba lub grupa liczb, zwana okresem ułamka, jest powtarzana w nieskończoność od określonego miejsca po przecinku).

Przykład 2

Na przykład okres ułamka okresowego $4,33333333333\dots$ to cyfra 3$, a okres ułamka $676,68349349\dots$ to grupa cyfr 349$.

Aby zachować zwięzłość przy pisaniu nieskończonych okresowych ułamków dziesiętnych, zwyczajowo zapisuje się kropkę raz, umieszczając ją w nawiasach. Na przykład ułamek okresowy $4,33333333333\dots$ jest zapisywany jako $4,(3)$, a ułamek okresowy $676,68349349\dots$ jest zapisywany jako $676,68(349)$.

Nieskończone okresowe ułamki dziesiętne uzyskuje się poprzez przekształcenie ułamków zwykłych, których mianowniki zawierają czynniki pierwsze inne niż 2 $ i 5 $, na ułamki dziesiętne.

Dowolny skończony ułamek dziesiętny (i liczbę całkowitą) można zapisać jako ułamek okresowy, dodając po prawej stronie nieskończoną liczbę cyfr $0$.

Przykład 3

Na przykład skończoną liczbę dziesiętną 45,12 $ można zapisać jako ułamek okresowy jako 45,12 (0) $, a liczbę całkowitą $ (74) $ jako nieskończoną okresową liczbę dziesiętną będzie to 74 (0) $.

W przypadku ułamków okresowych o okresie 9 należy zastosować przejście do innego zapisu ułamka okresowego o okresie 0 $. Tylko w tym celu kropkę 9 zastępuje się kropką $0$, a wartość kolejnej największej cyfry zwiększa się o 1$.

Przykład 4

Na przykład ułamek okresowy 7,45(9)$ można zastąpić ułamkiem okresowym 7,46(0)$ lub równoważnym ułamkiem dziesiętnym 7,46$.

Nieskończone dziesiętne ułamki okresowe są reprezentowane przez liczby wymierne. Innymi słowy, dowolny ułamek okresowy można przekształcić w ułamek zwykły, a każdy ułamek zwykły można przedstawić jako ułamek okresowy.

Zamiana ułamków zwykłych na skończone i nieskończone okresowe ułamki dziesiętne

Na ułamek dziesiętny można zamienić nie tylko zwykłe ułamki zwykłe o mianownikach 10, 100, \dots$.

W niektórych przypadkach pierwotny ułamek zwykły można łatwo sprowadzić do mianownika 10 $, 100 $ lub 1\000 $, po czym powstały ułamek można przedstawić jako ułamek dziesiętny.

Przykład 5

Aby zamienić ułamek $\frac(3)(5)$ na ułamek o mianowniku 10$, należy pomnożyć licznik i mianownik ułamka przez 2$, po czym otrzymamy $\frac(6)( 10)$, co nie jest trudne do przeliczenia na ułamek dziesiętny 0,6$.

W innych przypadkach stosuje się inną metodę konwersji ułamka zwykłego na dziesiętny):

licznik należy zastąpić ułamkiem dziesiętnym z dowolną liczbą zer po przecinku;

podziel licznik ułamka przez mianownik (dzielenie odbywa się jako dzielenie liczb naturalnych na kolumnę, a w ilorazie stawia się przecinek po zakończeniu dzielenia całej części dywidendy).

Przykład 6

Zamień ułamek $\frac(621)(4)$ na dziesiętny.

Rozwiązanie.

Przedstawmy liczbę 621 $ w liczniku jako ułamek dziesiętny. Aby to zrobić, dodaj przecinek dziesiętny i na początek dwa zera po nim. Następnie, jeśli to konieczne, możesz dodać więcej zer. Otrzymaliśmy więc 621,00 $.

Podzielmy liczbę 621,00 $ przez 4 $ w kolumnie:

Obrazek 1.

Podział osiągnął przecinek w dywidendzie, a reszta nie była równa zero. W takim przypadku wstaw przecinek dziesiętny do ilorazu i kontynuuj dzielenie w kolumnie, niezależnie od przecinków:

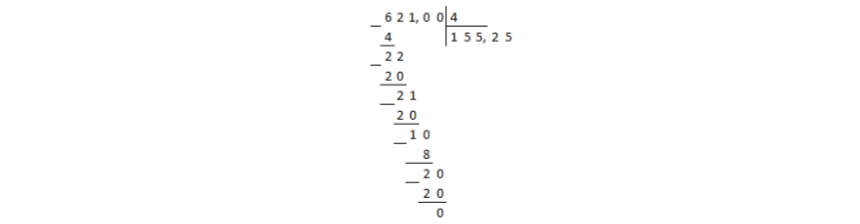
Rysunek 2.

Reszta wynosi zero, co oznacza koniec dzielenia.

Odpowiedź: $155,25$.

Możliwe jest, że przy dzieleniu licznika i mianownika ułamka zwykłego reszta nie da $0. W takim przypadku podział można kontynuować w nieskończoność. Począwszy od pewnego momentu reszty z dzielenia powtarzają się okresowo, co oznacza, że ​​powtarzają się również liczby w ilorazu. Z tego możemy wywnioskować, że ten ułamek zwykły zostanie zamieniony na nieskończony okresowy ułamek dziesiętny.

Przykład 7

Zamień ułamek $\frac(19)(44)$ na dziesiętny.

Rozwiązanie.)

Aby zamienić ułamek zwykły na dziesiętny, wykonaj długie dzielenie:

Rysunek 3.

Przy dzieleniu powtarzają się reszty 8$ i 36$, a w ilorazie powtarzają się także liczby 1$ i 8$. Zatem pierwotny ułamek zwykły $\frac(19)(44)$ został zamieniony na ułamek okresowy $\frac(19)(44)=0,43181818\dots =0,43(18)$.

Odpowiedź: $0,43(18)$.

Ogólny wniosek dotyczący zamiany ułamków zwykłych na dziesiętne:

jeśli mianownik da się rozłożyć na czynniki pierwsze, wśród których znajdą się tylko liczby $2$ i $5$, to taki ułamek można zamienić na końcowy ułamek dziesiętny;

jeśli oprócz liczb $2$ i $5$ rozwinięcie mianownika zawiera inne liczby pierwsze, wówczas taki ułamek jest zamieniany na nieskończony dziesiętny ułamek okresowy.

Zdarza się, że dla wygody obliczeń trzeba zamienić ułamek zwykły na dziesiętny i odwrotnie. Porozmawiamy o tym, jak to zrobić w tym artykule. Przyjrzyjmy się zasadom konwersji ułamków zwykłych na ułamki dziesiętne i odwrotnie, a także podaj przykłady.

Yandex.RTB R-A-339285-1

Rozważymy zamianę ułamków zwykłych na dziesiętne, zachowując określoną kolejność. Najpierw przyjrzyjmy się, jak ułamki zwykłe o mianowniku będącym wielokrotnością 10 są przekształcane na ułamki dziesiętne: 10, 100, 1000 itd. Ułamki zwykłe o takich mianownikach są w rzeczywistości bardziej uciążliwym zapisem ułamków dziesiętnych.

Następnie przyjrzymy się, jak zamienić ułamki zwykłe o dowolnym mianowniku, a nie tylko wielokrotnościach 10, na ułamki dziesiętne. Należy pamiętać, że podczas konwersji ułamków zwykłych na ułamki dziesiętne uzyskuje się nie tylko skończone ułamki dziesiętne, ale także nieskończone okresowe ułamki dziesiętne.

Zacznijmy!

Tłumaczenie ułamków zwykłych o mianownikach 10, 100, 1000 itd. do ułamków dziesiętnych

Po pierwsze, powiedzmy, że niektóre ułamki zwykłe wymagają pewnego przygotowania przed konwersją do postaci dziesiętnej. Co to jest? Przed liczbą w liczniku należy dodać tyle zer, aby liczba cyfr w liczniku była równa liczbie zer w mianowniku. Na przykład w przypadku ułamka 3100 liczbę 0 należy dodać raz na lewo od 3 w liczniku. Frakcja 610 zgodnie z zasadą podaną powyżej nie wymaga modyfikacji.

Spójrzmy na jeszcze jeden przykład, po którym sformułujemy regułę, która będzie szczególnie wygodna w użyciu na początku, podczas gdy nie ma dużego doświadczenia w konwertowaniu ułamków. Zatem ułamek 1610000 po dodaniu zer w liczniku będzie wyglądał jak 001510000.

Jak przekonwertować ułamek zwykły o mianowniku 10, 100, 1000 itd. do dziesiętnego?

Zasada zamiany ułamków zwykłych zwykłych na dziesiętne

1. Zapisz 0 i postaw po nim przecinek.
2. Liczbę zapisujemy z licznika, który otrzymaliśmy po dodaniu zer.

Przejdźmy teraz do przykładów.

Przykład 1: Konwersja ułamków zwykłych na dziesiętne

Zamieńmy ułamek zwykły 39 100 na ułamek dziesiętny.

Najpierw patrzymy na ułamek i widzimy, że nie ma potrzeby wykonywania żadnych działań przygotowawczych - liczba cyfr w liczniku pokrywa się z liczbą zer w mianowniku.

Zgodnie z zasadą zapisujemy 0, stawiamy po nim kropkę dziesiętną i zapisujemy liczbę z licznika. Otrzymujemy ułamek dziesiętny 0,39.

Spójrzmy na rozwiązanie innego przykładu na ten temat.

Przykład 2. Zamiana ułamków zwykłych na dziesiętne

Zapiszmy ułamek 105 10000000 jako ułamek dziesiętny.

Liczba zer w mianowniku wynosi 7, a licznik ma tylko trzy cyfry. Dodajmy jeszcze 4 zera przed liczbą w liczniku:

0000105 10000000

Teraz wpisujemy 0, stawiamy po nim kropkę dziesiętną i zapisujemy liczbę z licznika. Otrzymujemy ułamek dziesiętny 0,0000105.

Ułamki uwzględnione we wszystkich przykładach są zwykłymi ułamkami właściwymi. Ale jak zamienić ułamek niewłaściwy na dziesiętny? Powiedzmy od razu, że nie ma potrzeby przygotowania z dodawaniem zer dla takich ułamków. Sformułujmy regułę.

Zasada zamiany zwykłych ułamków niewłaściwych na dziesiętne

1. Zapisz liczbę znajdującą się w liczniku.
2. Przecinkiem dziesiętnym oddzielamy po prawej stronie tyle cyfr, ile jest zer w mianowniku ułamka pierwotnego.

Poniżej znajduje się przykład użycia tej reguły.

Przykład 3. Konwersja ułamków zwykłych na dziesiętne

Zamieńmy ułamek 56888038009 100000 ze zwykłego ułamka nieregularnego na dziesiętny.

Najpierw zapiszmy liczbę z licznika:

Teraz po prawej stronie oddzielamy pięć cyfr przecinkiem (liczba zer w mianowniku wynosi pięć). Otrzymujemy:

Kolejne pytanie, które naturalnie się pojawia, brzmi: jak zamienić liczbę mieszaną na ułamek dziesiętny, jeśli mianownikiem jej części ułamkowej jest liczba 10, 100, 1000 itd. Aby zamienić taką liczbę na ułamek dziesiętny, możesz skorzystać z poniższej reguły.

Zasada zamiany liczb mieszanych na dziesiętne

1. W razie potrzeby przygotowujemy część ułamkową liczby.
2. Zapisujemy całą część pierwotnej liczby i stawiamy po niej przecinek.
3. Liczbę z licznika części ułamkowej zapisujemy wraz z dodanymi zerami.

Spójrzmy na przykład.

Przykład 4: Konwersja liczb mieszanych na dziesiętne

Zamieńmy liczbę mieszaną 23 17 10000 na ułamek dziesiętny.

W części ułamkowej mamy wyrażenie 17 10000. Przygotujmy go i dodajmy jeszcze dwa zera po lewej stronie licznika. Otrzymujemy: 0017 10000.

Teraz zapisujemy całą część liczby i stawiamy po niej przecinek: 23, . .

Po przecinku zapisz liczbę z licznika wraz z zerami. Otrzymujemy wynik:

23 17 10000 = 23 , 0017

Zamiana ułamków zwykłych na ułamki okresowe skończone i nieskończone

Oczywiście można konwertować na ułamki dziesiętne i zwykłe o mianowniku różnym od 10, 100, 1000 itd.

Często ułamek można łatwo sprowadzić do nowego mianownika, a następnie zastosować regułę przedstawioną w pierwszym akapicie tego artykułu. Na przykład wystarczy pomnożyć licznik i mianownik ułamka 25 przez 2 i otrzymamy ułamek 410, który łatwo przeliczyć na postać dziesiętną 0,4.

Jednak ta metoda konwersji ułamka zwykłego na dziesiętny nie zawsze może być zastosowana. Poniżej zastanowimy się, co zrobić, jeśli nie można zastosować rozważanej metody.

Całkowicie nowym sposobem zamiany ułamka zwykłego na dziesiętny jest podzielenie licznika przez mianownik za pomocą kolumny. Ta operacja jest bardzo podobna do dzielenia liczb naturalnych przez kolumnę, ale ma swoje własne cechy.

Podczas dzielenia licznik jest przedstawiany jako ułamek dziesiętny – po prawej stronie ostatniej cyfry licznika stawia się przecinek i dodaje się zera. W otrzymanym ilorazie kropkę dziesiętną umieszcza się, gdy kończy się dzielenie części całkowitej licznika. Jak dokładnie działa ta metoda, stanie się jasne po zapoznaniu się z przykładami.

Przykład 5. Konwersja ułamków zwykłych na dziesiętne

Zamieńmy ułamek zwykły 621 4 na postać dziesiętną.

Przedstawmy liczbę 621 z licznika jako ułamek dziesiętny, dodając kilka zer po przecinku. 621 = 621,00

Teraz podzielmy 621,00 przez 4 za pomocą kolumny. Pierwsze trzy kroki dzielenia będą takie same jak przy dzieleniu liczb naturalnych i otrzymamy.

Kiedy dochodzimy do przecinka w dzielnej, a reszta jest różna od zera, stawiamy przecinek w ilorazu i kontynuujemy dzielenie, nie zwracając już uwagi na przecinek w dywidendzie.

W rezultacie otrzymujemy ułamek dziesiętny 155, 25, który jest wynikiem odwrócenia ułamka zwykłego 621 4

621 4 = 155 , 25

Spójrzmy na inny przykład wzmocnienia materiału.

Przykład 6. Konwersja ułamków zwykłych na dziesiętne

Odwróćmy ułamek zwykły 21 800.

Aby to zrobić, podziel ułamek 21 000 na kolumnę przez 800. Dzielenie całej części zakończy się na pierwszym etapie, więc zaraz po nim stawiamy przecinek w ilorazu i kontynuujemy dzielenie, nie zwracając uwagi na przecinek w dzielnej, aż do momentu, gdy otrzymamy resztę równą zero.

W rezultacie otrzymaliśmy: 21 800 = 0,02625.

Co jednak, jeśli przy dzieleniu nadal nie otrzymamy reszty równej 0. W takich przypadkach dzielenie można kontynuować w nieskończoność. Jednakże, począwszy od pewnego etapu, pozostałości będą powtarzane okresowo. W związku z tym liczby w ilorazu zostaną powtórzone. Oznacza to, że ułamek zwykły jest zamieniany na dziesiętny nieskończony ułamek okresowy. Zilustrujmy to przykładem.

Przykład 7. Konwersja ułamków zwykłych na dziesiętne

Zamieńmy ułamek zwykły 19 44 na ułamek dziesiętny. Aby to zrobić, wykonujemy dzielenie według kolumn.

Widzimy, że podczas dzielenia powtarzają się reszty 8 i 36. W tym przypadku liczby 1 i 8 powtarzają się w ilorazie. Jest to okres w ułamku dziesiętnym. Podczas nagrywania liczby te są umieszczane w nawiasach.

W ten sposób pierwotny ułamek zwykły zostaje przekształcony w nieskończony okresowy ułamek dziesiętny.

19 44 = 0 , 43 (18) .

Zobaczmy nieredukowalny ułamek zwykły. Jaką formę przyjmie? Które ułamki zwykłe zamienia się na skończone ułamki dziesiętne, a które na nieskończone ułamki okresowe?

Załóżmy najpierw, że jeśli ułamek można sprowadzić do jednego z mianowników 10, 100, 1000..., to będzie on miał postać końcowego ułamka dziesiętnego. Aby ułamek został zredukowany do jednego z tych mianowników, jego mianownik musi być dzielnikiem co najmniej jednej z liczb 10, 100, 1000 itd. Z zasad rozkładania liczb na czynniki pierwsze wynika, że ​​dzielnikiem liczb jest 10, 100, 1000 itd. musi, po rozłożeniu na czynniki pierwsze, zawierać tylko liczby 2 i 5.

Podsumujmy co zostało powiedziane:

1. Ułamek zwykły można sprowadzić do końcowego ułamka dziesiętnego, jeśli jego mianownik można rozłożyć na czynniki pierwsze 2 i 5.
2. Jeżeli oprócz liczb 2 i 5 w rozwinięciu mianownika znajdują się inne liczby pierwsze, ułamek jest redukowany do postaci nieskończonej okresowej części dziesiętnej.

Podajmy przykład.

Przykład 8. Konwersja ułamków zwykłych na dziesiętne

Który z tych ułamków 47 20, 7 12, 21 56, 31 17 zamienia się na końcowy ułamek dziesiętny, a który tylko na okresowy. Odpowiedzmy na to pytanie bez bezpośredniej konwersji ułamka zwykłego na dziesiętny.

Ułamek 47 20, jak łatwo zauważyć, mnożąc licznik i mianownik przez 5, redukuje się do nowego mianownika 100.

47 20 = 235 100. Z tego wnioskujemy, że ułamek ten jest konwertowany na końcowy ułamek dziesiętny.

Rozłożenie mianownika ułamka na czynniki daje 12 = 2 · 2 · 3. Ponieważ czynnik pierwszy 3 różni się od 2 i 5, ułamka tego nie można przedstawić jako skończonego ułamka dziesiętnego, ale będzie on miał postać nieskończonego ułamka okresowego.

Najpierw należy zmniejszyć ułamek 21 56. Po redukcji przez 7 otrzymujemy ułamek nieredukowalny 3 8, którego mianownik jest rozkładany na czynniki w celu uzyskania 8 = 2 · 2 · 2. Jest to zatem ułamek dziesiętny skończony.

W przypadku ułamka 31 17 mianownikiem jest sama liczba pierwsza 17. W związku z tym ułamek ten można przekształcić w nieskończony okresowy ułamek dziesiętny.

Ułamka zwykłego nie można zamienić na nieskończony i nieokresowy ułamek dziesiętny

Powyżej mówiliśmy tylko o skończonych i nieskończonych ułamkach okresowych. Ale czy każdy zwykły ułamek można przekształcić w nieskończony ułamek nieokresowy?

Odpowiadamy: nie!

Ważny!

Podczas konwersji ułamka nieskończonego na ułamek dziesiętny wynikiem jest albo skończona liczba dziesiętna, albo nieskończona okresowa liczba dziesiętna.

Reszta dzielenia jest zawsze mniejsza od dzielnika. Innymi słowy, zgodnie z twierdzeniem o podzielności, jeśli podzielimy jakąś liczbę naturalną przez liczbę q, to ​​reszta z dzielenia w żadnym wypadku nie może być większa niż q-1. Po zakończeniu podziału możliwa jest jedna z następujących sytuacji:

1. Otrzymujemy resztę równą 0 i na tym dzielenie się kończy.
2. Otrzymujemy resztę, która jest powtarzana przy kolejnym dzieleniu, w wyniku czego otrzymujemy nieskończony ułamek okresowy.

Nie ma innej możliwości zamiany ułamka zwykłego na dziesiętny. Powiedzmy również, że długość okresu (liczba cyfr) nieskończonego ułamka okresowego jest zawsze mniejsza niż liczba cyfr w mianowniku odpowiedniego ułamka zwykłego.

Zamiana ułamków dziesiętnych na ułamki zwykłe

Teraz czas przyjrzeć się odwrotnemu procesowi zamiany ułamka dziesiętnego na ułamek zwykły. Sformułujmy regułę tłumaczenia, która obejmuje trzy etapy. Jak zamienić ułamek dziesiętny na ułamek zwykły?

Zasada zamiany ułamków dziesiętnych na zwykłe

1. W liczniku zapisujemy liczbę z pierwotnego ułamka dziesiętnego, odrzucając przecinek i wszystkie zera po lewej stronie, jeśli występują.
2. W mianowniku zapisujemy jedynkę i tyle zer, ile jest cyfr po przecinku w pierwotnym ułamku dziesiętnym.
3. Jeśli to konieczne, zmniejsz powstałą ułamek zwykły.

Przyjrzyjmy się zastosowaniu tej zasady na przykładach.

Przykład 8. Zamiana ułamków dziesiętnych na zwykłe

Wyobraźmy sobie liczbę 3,025 jako ułamek zwykły.

1. Do licznika wpisujemy sam ułamek dziesiętny, odrzucając przecinek: 3025.
2. W mianowniku piszemy jeden, a po nim trzy zera - dokładnie tyle cyfr zawiera się w pierwotnym ułamku po przecinku: 3025 1000.
3. Powstały ułamek 3025 1000 można zmniejszyć o 25, otrzymując: 3025 1000 = 121 40.

Przykład 9. Konwersja ułamków dziesiętnych na ułamki zwykłe

Zamieńmy ułamek 0,0017 z dziesiętnego na zwykły.

1. W liczniku zapisujemy ułamek 0, 0017, odrzucając przecinek i zera po lewej stronie. Okazuje się, że będzie to 17.
2. W mianowniku zapisujemy jedynkę, a po niej cztery zera: 17 10000. Ułamek ten jest nieredukowalny.

Jeśli ułamek dziesiętny ma część całkowitą, wówczas taki ułamek można natychmiast przekształcić w liczbę mieszaną. Jak to zrobić?

Sformułujmy jeszcze jedną zasadę.

Zasada zamiany ułamków dziesiętnych na liczby mieszane.

1. Liczbę przed przecinkiem ułamkowym zapisuje się jako część całkowitą liczby mieszanej.
2. W liczniku zapisujemy liczbę po przecinku ułamka zwykłego, odrzucając zera po lewej stronie, jeśli takie istnieją.
3. Do mianownika części ułamkowej dodajemy jeden i tyle zer, ile jest cyfr po przecinku w części ułamkowej.

Weźmy przykład

Przykład 10. Konwersja ułamka dziesiętnego na liczbę mieszaną

Wyobraźmy sobie ułamek 155, 06005 jako liczbę mieszaną.

1. Liczbę 155 zapisujemy jako część całkowitą.
2. W liczniku zapisujemy liczby po przecinku, odrzucając zero.
3. W mianowniku zapisujemy jeden i pięć zer

Nauczmy się liczby mieszanej: 155 6005 100000

Część ułamkową można zmniejszyć o 5. Skracamy go i otrzymujemy efekt końcowy:

155 , 06005 = 155 1201 20000

Zamiana nieskończonych okresowych ułamków dziesiętnych na ułamki zwykłe

Spójrzmy na przykłady zamiany okresowych ułamków dziesiętnych na ułamki zwykłe. Zanim zaczniemy, wyjaśnijmy: każdy okresowy ułamek dziesiętny można zamienić na ułamek zwykły.

Najprostszy przypadek ma miejsce, gdy okres ułamka wynosi zero. Ułamek okresowy z kropką zerową zastępuje się końcowym ułamkiem dziesiętnym, a proces odwracania takiego ułamka sprowadza się do odwracania końcowego ułamka dziesiętnego.

Przykład 11. Konwersja okresowego ułamka dziesiętnego na ułamek zwykły

Odwróćmy ułamek okresowy 3, 75 (0).

Eliminując zera po prawej stronie, otrzymujemy końcowy ułamek dziesiętny 3,75.

Przekształcając ten ułamek na ułamek zwykły za pomocą algorytmu omówionego w poprzednich akapitach, otrzymujemy:

3 , 75 (0) = 3 , 75 = 375 100 = 15 4 .

A co jeśli okres ułamka jest różny od zera? Część okresową należy traktować jako sumę wyrazów postępu geometrycznego, który maleje. Wyjaśnijmy to na przykładzie:

0 , (74) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .

Istnieje wzór na sumę wyrazów nieskończonego malejącego postępu geometrycznego. Jeśli pierwszym wyrazem ciągu jest b, a mianownik q jest taki, że 0< q < 1 , то сумма равна b 1 - q .

Przyjrzyjmy się kilku przykładom wykorzystania tej formuły.

Przykład 12. Konwersja okresowego ułamka dziesiętnego na ułamek zwykły

Mamy ułamek okresowy 0, (8) i musimy go zamienić na ułamek zwykły.

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . .

Tutaj mamy nieskończony malejący postęp geometryczny z pierwszym wyrazem 0, 8 i mianownikiem 0, 1.

Zastosujmy wzór:

0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 - 0 , 1 = 0 , 8 0 , 9 = 8 9

Jest to wymagany ułamek zwykły.

Aby skonsolidować materiał, rozważ inny przykład.

Przykład 13. Konwersja okresowego ułamka dziesiętnego na ułamek zwykły

Odwróćmy ułamek 0, 43 (18).

Najpierw zapisujemy ułamek jako sumę nieskończoną:

0 , 43 (18) = 0 , 43 + (0 , 0018 + 0 , 000018 + 0 , 00000018 . .)

Spójrzmy na terminy w nawiasach. Ten postęp geometryczny można przedstawić w następujący sposób:

0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 - 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .

Wynik dodajemy do ułamka końcowego 0, 43 = 43 100 i otrzymujemy wynik:

0 , 43 (18) = 43 100 + 18 9900

Po dodaniu tych ułamków i skróceniu otrzymujemy ostateczną odpowiedź:

0 , 43 (18) = 19 44

Na zakończenie tego artykułu powiemy, że nieokresowych nieskończonych ułamków dziesiętnych nie można przekształcić w ułamki zwykłe.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Operacja podziału zakłada udział kilku głównych elementów. Pierwszą z nich jest tzw. dywidenda, czyli liczba podlegająca procedurze podziału. Drugi to dzielnik, czyli liczba, według której przeprowadza się dzielenie. Trzeci to iloraz, czyli wynik operacji dzielenia dywidendy przez dzielnik.

Wynik podziału

Najprostszym wynikiem, jaki można uzyskać, stosując dwie dodatnie liczby całkowite jako dzielną i dzielnik, jest kolejna dodatnia liczba całkowita. Na przykład przy dzieleniu 6 przez 2 iloraz będzie równy 3. Taka sytuacja jest możliwa, jeśli dywidenda jest dzielnikiem, to znaczy jest przez nią dzielona bez reszty.

Istnieją jednak inne opcje, gdy nie można przeprowadzić operacji dzielenia bez reszty. W takim przypadku liczba niecałkowita staje się ilorazem, który można zapisać jako kombinację liczby całkowitej i części ułamkowej. Na przykład przy dzieleniu 5 przez 2 iloraz wynosi 2,5.

Numer w okresie

Jedną z opcji, która może wyniknąć, jeśli dywidenda nie jest wielokrotnością dzielnika, jest tzw. liczba w okresie. Może powstać w wyniku podziału, jeśli iloraz okaże się nieskończenie powtarzającym się zbiorem liczb. Przykładowo liczba w kropce może pojawić się przy dzieleniu liczby 2 przez 3. W tej sytuacji wynik w postaci ułamka dziesiętnego zostanie wyrażony jako kombinacja nieskończonej liczby 6 cyfr po przecinku.

Aby wskazać wynik takiego dzielenia, wymyślono specjalny sposób zapisywania liczb w kropce: liczbę taką oznacza się poprzez umieszczenie powtarzającej się cyfry w nawiasie. Na przykład wynik dzielenia 2 przez 3 przy użyciu tej metody można zapisać jako 0,(6). Zapis ten stosuje się również wtedy, gdy powtarza się tylko część liczby wynikającej z dzielenia.

Na przykład, dzieląc 5 przez 6, wynikiem będzie liczba okresowa w postaci 0,8 (3). Stosowanie tej metody jest po pierwsze skuteczniejsze w porównaniu z próbą zapisania całości lub części cyfr liczby w kropce, a po drugie charakteryzuje się większą dokładnością w porównaniu z inną metodą przesyłania takich liczb - zaokrąglaniem, a ponadto pozwala na odróżnienie liczb okresowych od dokładnego ułamka dziesiętnego o odpowiedniej wartości podczas porównywania wielkości tych liczb. Zatem na przykład oczywiste jest, że 0,(6) jest znacznie większe niż 0,6.